The product of two regular quaternions $\pmb{r} = r_0 + \vec{r}$ and $\pmb{v} = 0 + \vec{v}$ is:
$$\begin{align} \pmb{r}\vec{v} &= \big( r_0 + \vec{r}\big)\big(\vec{v} \big) \\ &= \big( r_0 + r_x\vec{i}+ r_y\vec{j} + r_z\vec{k}\big)\big(v_x\vec{i}+ v_y\vec{j} + v_z\vec{k} \big) \\ \\ &= r_{0}v_{x}\vec{i} + r_{0}v_{y}\vec{j} + r_{0}v_{z}\vec{k} \\ &\quad - r_{x}v_{x} + r_{x}v_{y}\vec{k} - r_{x}v_{z}\vec{j} \\ &\quad - r_{y}v_{x}\vec{k} - r_{y}v_{y} + r_{y}v_{z}\vec{i} \\ &\quad + r_{z}v_{x}\vec{j} - r_{z}v_{y}\vec{i} - r_{z}v_{z} \tag{1} \end{align}$$Rearranging the terms in equation $\big(1\big)$ as follows:
$$\begin{align} \pmb{r}\vec{v} &= -\big(r_{x}v_{x} + r_{y}v_{y} + r_{z}v_{z}\big) \\ &\quad+ r_{0}\big(v_{x}\vec{i} + v_{y}\vec{j} + v_{z}\vec{k}\big) \\ &\quad+ \big(r_{y}v_{z} - r_{z}v_{y}\big)\vec{i} + \big(r_{z}v_{x} - r_{x}v_{z} \big)\vec{j} + \big( r_{x}v_{y} - r_{y}v_{x}\big)\vec{k}\tag{2} \\ \\ &= - \vec{r}\cdot\vec{v} + r_{0}\vec{v} + \vec{r} \times \vec{v} \tag{3} \end{align}$$Right multiplying equation $\big(3\big)$ by the conjugate $\pmb{r}^{*} = r_{0} - \vec{r}$ gives:
$$\begin{align} \pmb{r}\vec{v}\pmb{r}^{*} &= \big(- \vec{r}\cdot\vec{v} + r_{0}\vec{v} + \vec{r} \times \vec{v}\big)\big(r_{0} - \vec{r} \big) \\ &= -(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \big(\vec{v}r_{0} + (\vec{r} \times \vec{v})\big)r_{0} + \big(\vec{v}r_{0} + (\vec{r} \times \vec{v})\big)(-\vec{r}) \\ &= -(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \vec{v}r_{0}^2 + (\vec{r} \times \vec{v})r_{0} +\vec{v}r_{0}(-\vec{r} ) + (\vec{r} \times \vec{v})(-\vec{r})\tag{4} \\ \end{align}$$Expanding and rearranging the term $(\vec{r} \times \vec{v})(-\vec{r})$ and letting $\vec{m} = \vec{r} \times \vec{v}$:
$$\begin{align} (\vec{r} \times \vec{v})(-\vec{r})&= \big(r_{y}v_{z} - r_{z}v_{y}\big)\vec{i}\big( r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big) \\ &\quad+ \big(r_{z}v_{x} - r_{x}v_{z} \big)\vec{j}\big( r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big) \\ &\quad+ \big( r_{x}v_{y} - r_{y}v_{x}\big)\vec{k}\big(r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big)\tag{5} \\ \\ &= m_{x}r_0\vec{i} + m_{x}r_x - m_{x}r_y\vec{k} + m_{x}r_z\vec{j} \\ &\quad+ m_{y}r_0\vec{j} + m_{y}r_x\vec{k} + m_{y}r_y - m_{y}r_z\vec{i} \\ &\quad+ m_{z}r_0\vec{k} - m_{z}r_x\vec{j} + m_{z}r_y\vec{i} + m_{z}r_z\tag{6} \\ \\ &= m_{x}r_x + m_{y}r_y + m_{z}r_z \\ &\quad+ r_0\big(m_{x}\vec{i} + m_{y}\vec{j} + m_{z}\vec{k}\big) \\ &\quad+ \big(m_{z}r_y - m_{y}r_z\big)\vec{i} + \big(m_{x}r_z - m_{z}r_x \big)\vec{j} + \big(m_{y}r_x - m_{x}r_y \big)\vec{k}\tag{7} \\ \\ &= \big(\vec{r} \times \vec{v}\big) \cdot \vec{r} + r_{0}\big(\vec{r} \times \vec{v}\big) - \big(\vec{r} \times \vec{v}\big)\times\vec{r}\tag{8} \end{align}$$The following term has this vector triple product expansion:
$$\begin{align} \big(\vec{r} \times \vec{v}\big)\times\vec{r} &= -\big(\vec{r}\cdot\vec{v}\big)\vec{r} + \big(\vec{r}\cdot\vec{r}\big)\vec{v} \\ &= -\big(\vec{r}\cdot\vec{v}\big)\vec{r} + \Vert\vec{r}\Vert^2\vec{v} \end{align}$$Since $\big(\vec{r} \times \vec{v}\big) \cdot \vec{r} = 0$ then $(8)$ becomes:
$$(\vec{r} \times \vec{v})(-\vec{r} )= r_{0}\big(\vec{r} \times \vec{v}\big)+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{9}$$Expanding and rearranging $\vec{v}(-\vec{r})$ in the term $\vec{v}r_{0}(-\vec{r})$:
$$\begin{align} \vec{v}(-\vec{r}) &= \big(v_{x}\vec{i} + v_{y}\vec{j} + v_{z}\vec{k}\big)\big(-r_{x}\vec{i} - r_{y}\vec{j} - r_{z}\vec{z} \big) \\ &= v_{x}r_{x} - v_{x}r_{y}\vec{k} + v_{x}r_{z}\vec{j} \\ &\quad v_{y}r_{x}\vec{k} + v_{y}r_{y} - v_{y}r_{z}\vec{i} \\ &\quad -v_{z}r_{x}\vec{j} + v_{z}r_{y}\vec{i} + v_{z}r_{z} \\ \\ &= \big(v_{x}r_{x} + v_{y}r_{y} + v_{z}r_{z}\big) \\ &\quad +\big(-v_{y}r_{z} + v_{z}r_{y}\big)\vec{i} + \big(-v_{z}r_{x} + v_{x}r_{z}\big)\vec{j}+\big(-v_{x}r_{y} + v_{y}r_{x}\big)\vec{k} \\ \\ &= \vec{v}\cdot \vec{r} - \vec{v} \times \vec{r} \\ &= \vec{r}\cdot \vec{v} + \vec{r} \times \vec{v}\tag{10} \end{align}$$The terms $\vec{v}r_{0}(-\vec{r}) +(\vec{r} \times \vec{v})(-\vec{r})$ in $(4)$ then become:
$$\begin{align} \vec{v}r_{0}(-\vec{r}) +(\vec{r} \times \vec{v})(-\vec{r}) &= r_{0}(\vec{r}\cdot \vec{v}) + r_{0}(\vec{r} \times \vec{v}) +r_{0}\big(\vec{r} \times \vec{v}\big)+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v} \\ &= r_{0}(\vec{r}\cdot \vec{v}) + 2r_{0}(\vec{r} \times \vec{v})+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{11} \end{align}$$Substituting $\big(11\big)$ into equation $\big(4\big)$:
$$-(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \vec{v}r_{0}^2 + (\vec{r} \times \vec{v})r_{0} +r_{0}(\vec{r}\cdot \vec{v}) + 2r_{0}(\vec{r} \times \vec{v})+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{12}$$Reducing $\big(12\big)$ gives the pure quaternion:
$$\pmb{r}\vec{v}\pmb{r}^{*} = \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\vec{v} +2\big(\vec{r}\cdot\vec{v}\big)\vec{r} + 2r_{0}\big(\vec{r}\times\vec{v}\big)\tag{13}$$Next we need to find out what rotation the unit quaternion $\pmb{r}$ represents. Substituting $\vec{r}$ for $\vec{v}$ in $\big(13\big)$ makes $\vec{v} = \vec{r}$ collinear with the axis of rotation and yields:
$$\begin{align} \pmb{r}\vec{v}\pmb{r}^{*} &= \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\vec{v} +2\big(\vec{r}\cdot\vec{v}\big)\vec{r} + 2r_{0}\big(\vec{r}\times\vec{v}\big)\\ &= \big(r_{0}^2+\Vert\vec{r}\Vert^2\big)\vec{r}\\ &= \vec{r}\tag{14} \end{align}$$As it should, $\pmb{r}\vec{v}\pmb{r}^{*}$ remains the same as $\vec{r}$ after the rotation.
Finally, we need to determine the angle of rotation $\theta$. Let the vector $\vec{v}$ be perpendicular to the axis of rotation and then turned into a vector $\vec{{v}^{'}}$ making an angle $\theta$ with $\vec{v}$. In Figure 1 the position vector $\vec{a}$ is associated with $\vec{v}$ and then choosing $\vec{v} = \vec{r} \times \vec{a}$ where $\vec{a}$ is not parallel to $\vec{r}$ gives:
$$\vec{{v}^{'}} = \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\big(\vec{r} \times \vec{a}\big) +2\big(\vec{r}\cdot\big(\vec{r} \times \vec{a}\big)\big)\vec{r} + 2r_{0}\big(\vec{r}\times\big(\vec{r} \times \vec{a}\big)\big)\tag{15}$$We find that
$$\begin{align} \vec{v}\cdot\vec{{v}^{'}} &=\big(\vec{r} \times \vec{a}\big)\cdot\Big( \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\big(\vec{r} \times \vec{a}\big) +2\big(\vec{r}\cdot\big(\vec{r} \times \vec{a}\big)\big)\vec{r} + 2r_{0}\big(\vec{r}\times\big(\vec{r} \times \vec{a}\big)\big) \Big) \\ &= \big(r_{0}^{2} - \Vert\vec{r}\Vert^{2} \big)\Vert \vec{r} \times \vec{a} \Vert^{2}\\ &= \big(r_{0}^{2} - \Vert\vec{r}\Vert^{2} \big)\Vert v \Vert^{2}\tag{16} \end{align}$$Since $\Vert \vec{{v}^{'}} \Vert = \Vert \vec{v} \Vert$ and $\vec{v}\cdot\vec{{v}^{'}} = \Vert \vec{{v}^{'}} \Vert \Vert \vec{v} \Vert\cos{(\theta)}$ then
$$r_{0}^{2} - \Vert\vec{r}\Vert^{2} = \cos{(\theta)}\tag{17}$$Noting that $\pmb{r}$ is a unit quaternion then $r_{0}^{2} + \Vert\vec{r}\Vert^{2} = 1$ and this is added to $\big(17\big)$:
$$\begin{align} r_{0}^{2} + \Vert\vec{r}\Vert^{2} + r_{0}^{2} - \Vert\vec{r}\Vert^{2} &= 1 + \cos{(\theta)}\\ 2r_{0}^{2} &= 1 + \cos{(\theta)}\tag{18} \end{align}$$Using the trigonometric half-angle formula $\cos^2{\Big(\frac{\theta}{2}\Big)} = \frac{1 + \cos{(\theta)}}{2}$ on $\big(18\big)$ gives:
$$r_{0} = \pm\cos{\Big(\frac{\theta}{2}\Big)}\tag{19}$$Now if $\big(17\big)$ is subtracted from $r_{0}^{2} + \Vert\vec{r}\Vert^{2} = 1$ then:
$$\begin{align} r_{0}^{2} + \Vert\vec{r}\Vert^{2} - r_{0}^{2} + \Vert\vec{r}\Vert^{2} &= 1 - \cos{(\theta)}\\ 2\Vert\vec{r}\Vert^{2} &= 1 - \cos{(\theta)}\tag{20} \end{align}$$Using the trigonometric half-angle formula $\sin^2{\Big(\frac{\theta}{2}\Big)} = \frac{1 - \cos{(\theta)}}{2}$ on $\big(20\big)$ gives:
$$\Vert\vec{r}\Vert= \sin{\Big(\frac{\theta}{2}\Big)}\tag{21}$$Let $\vec{u}$ be the unit direction vector of the axis of rotation and $\vec{r}$:
$$\vec{r} = \pm\sin{\Big(\frac{\theta}{2}\Big)}\vec{u}\tag{22}$$Finally
$$\pmb{r} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{u}\tag{23}$$Using equations $(13)$, $(19)$ and $(22)$ with the trigonometric identities:
$$\begin{align} \cos^{2}{\Big(\frac{\theta}{2}\Big)} - \sin^{2}{\Big(\frac{\theta}{2}\Big)} &= \cos{\big(\theta\big)}\\ 2\sin{\Big(\frac{\theta}{2}\Big)}\cos{\Big(\frac{\theta}{2}\Big)} &= \sin{\big(\theta\big)}\\ \sin^2{\Big(\frac{\theta}{2}\Big)} &= \frac{1 - \cos{(\theta)}}{2} \end{align}$$we obtain the Rodrigues' rotation formula:
$$\begin{align} \vec{{v}^{'}} &=\bigg( \cos^2{\Big(\frac{\theta}{2}\Big)} - \sin^{2}{\Big(\frac{\theta}{2}\Big)} \bigg)\vec{v} + 2\cos{\Big(\frac{\theta}{2}\Big)}\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{u} \times \vec{v} \Big)+ 2\sin^2{\Big(\frac{\theta}{2}\Big)}\Big( \vec{u}\cdot \vec{v}\Big)\vec{u}\\ &= \cos{(\theta)}\vec{v} + \sin{(\theta)}\big(\vec{u} \times \vec{v}\big) + \big(1 - \cos{(\theta)}\big)\big(\vec{u} \cdot \vec{v}\big)\vec{u}\tag{24} \end{align}$$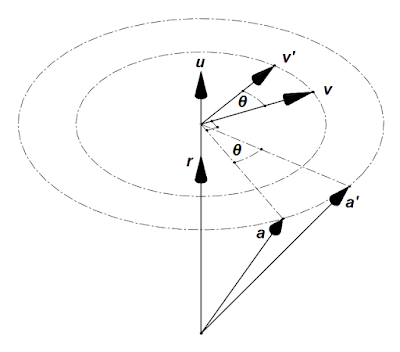
No comments:
Post a Comment