Unit Dual Quaternions, Line Transformations and Plücker Coordinates

BEWARE! THIS DRAFT HAS SOME SYMBOLS THAT DO NOT MATCH THOSE WE HAVE PREVIOUSLY USED. THE LETTER USED FOR TRANSLATION WAS $\vec{d}$ BUT HERE IT IS $\vec{t}$. THE SYMBOL FOR PARALLEL TRANSLATION TO THE AXIS WAS $\vec{d_{\Vert}}$ BUT HERE IT IS $\vec{d}$ AND THEREFORE $d = \Vert\vec{d}\Vert$ SO $\vec{d} = d\vec{l}$.

In Parallelograms, Plücker Coordinates and Dual Numbers we had a line $L$ with Plücker coordinates $\big(\vec{l}, \vec{m} \big)$ where $\vec{l}$ is a unit vector in the direction of line $L$ and $\vec{m} = \vec{p}\times\vec{l}$ where $\vec{p}$ can be chosen perpendicular to $L$ so $\vec{l}\cdot\vec{m} = 0$. Let the dual quaternion of these Plücker coordinates be:

$$\pmb{l} + \epsilon\pmb{m} = \vec{l} + \epsilon\vec{m}\tag{1}$$

The standard dual quaternion $\pmb{r_0} + \frac{\epsilon}{2}\vec{t}\pmb{r_0}$ for translation and rotation is not suited for Plücker Coordinates since it assumes a rotation axis through the origin and that means $\vec{p_{\bot}} = 0$ and $\vec{m} = 0$ which isn't what we want. What we want is this displacement to occur around axis $\mathrm{L}$ which does not pass through the origin but does pass through some point $\mathrm{P}$. We can obtain the dual quaternion for this axis offset by $\vec{p}$ by applying the translation dual quaternion $1 + \epsilon\frac{\vec{p}}{2}$ to the rotation dual quaternion $\pmb{\hat{r}}$ for the unit vector $\vec{l}$. However, from the post Unit Dual Quaternion For Translation And Rotation we can simply change this unit dual quaternion into the regular unit rotation quaternion $\pmb{r_0}$:

$$\pmb{\hat{r}} = \pmb{r_0} + \epsilon(0)$$ Recall that a regular rotation quaternion in terms of $\theta$ was derived in Extracting the Cross and Dot Products from the Quaternion Rotation Operator and for the unit vector $\vec{l}$ would be:

$$\pmb{r_0} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l}$$

Since this will be a transformation operation of the regular quaternion $\pmb{r_0}$, this quaternion has to be multiplied on both sides by the translation quaternion. We have seen this "quaternion sandwich operation" before with rotations but now we are doing it with a translation. The left side is multiplied by $1 + \epsilon\frac{\vec{p}}{2}$ and right is multiplied by the conjugate $1 - \epsilon\frac{\vec{p}}{2}$:

$$\begin{align} \Big(1 + &\epsilon\frac{\vec{p}}{2} \Big)\pmb{r_0}\Big(1 - \epsilon\frac{\vec{p}}{2} \Big) = \Big(1 + \epsilon\frac{\vec{p}}{2} \Big)\Big( \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l}\Big) \Big(1 - \epsilon\frac{\vec{p}}{2} \Big)\\ &= \bigg(\cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \frac{\epsilon}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{p} + \frac{\epsilon}{2}\sin{\Big(\frac{\theta}{2}\Big)}\vec{p}\vec{l}\bigg)\Big(1 - \epsilon\frac{\vec{p}}{2} \Big)\\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \frac{\epsilon}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{p} + \frac{\epsilon}{2}\sin{\Big(\frac{\theta}{2}\Big)}\vec{p}\vec{l} - \frac{\epsilon}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{p} - \frac{\epsilon}{2}\sin{\Big(\frac{\theta}{2}\Big)}\vec{l}\vec{p} \\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{p} \times \vec{l}\Big) \tag{2} \end{align}$$

However, to obtain a general (e.g. screw) displacement dual qauternion, we need to use another translation quaternion, $1 + \epsilon\frac{\vec{d}}{2}$, for the displacement $\vec{d}$ parallel to the rotation axis $L$ to equation $(2)$. Here we are concatenating/combine operations instead of transforming one operation, so there is only a simple one-side multiplication that needs to be done.

$$\begin{align} \bigg(1 + &\epsilon\frac{\vec{d}}{2}\bigg)\bigg( \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{p} \times \vec{l}\Big) \bigg) \\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\bigg(\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{p} \times \vec{l}\Big) + \frac{1}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{d} + \frac{1}{2}\sin{\Big(\frac{\theta}{2}\Big)}\vec{d}\vec{l}\bigg)\tag{3} \end{align}$$ and since $\vec{d}$ is parrallel to $\vec{l}$ then $\vec{d}\vec{l} = \big( \vec{d}\times\vec{l}\big) - \vec{d}\cdot\vec{l} = -d$ and equation $(3)$ becomes

$$\begin{align} & \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\bigg(\sin{\Big(\frac{\theta}{2}\Big)}\vec{m} + \frac{\vec{d}}{2}\cos{\Big(\frac{\theta}{2}\Big)} - \frac{d}{2}\sin{\Big(\frac{\theta}{2}\Big)}\bigg)\\ &= \cos{\Big(\frac{\theta}{2}\Big)} - \epsilon\frac{d}{2}\sin{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\Big(\sin{\Big(\frac{\theta}{2}\Big)}\vec{m} + \frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{l} \Big)\tag{4} \end{align}$$

AN ALTERNATIVE GEOMETRIC DERIVATION OF EQUATION $(4)$

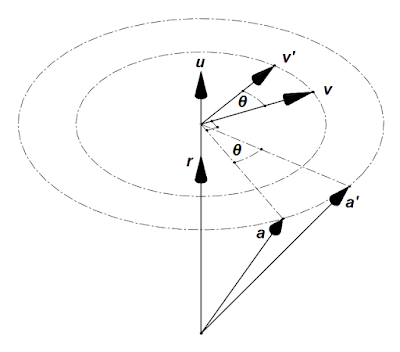
In Figure 1, the screw axis $\mathrm{L}$ has unit direction vector $\vec{l}$ and is represented by Plücker coordinates $(\vec{m}, \vec{l})$ where $\vec{m} = \vec{p}\times\vec{l}$ and $\vec{p}$ is from the origin and can be to any point $\mathrm{P}$ on line $\mathrm{L}$. The following formulas are general for any point $\mathrm{P}$ but we will choose $\vec{p}$ perpendicular to $\mathrm{L}$ so that $\vec{p} = \vec{p}_{\bot}$. Furthermore, $\vec{t}$ is the translation vector of any point by the screw displacement so the distance traveled parallel to $\mathrm{L}$ is $d = \vec{t}\cdot\vec{l}$.

FIGURE 1

To find $\vec{m}$ in terms of the screw displacement, start by screw displacing the origin point of the coordinate system at the tail of $\vec{p}_{\bot}$ as shown in Figure 1. This establishes the geometry we need to work with in finding the equation for the location of point $\mathrm{P}$ at the tip of $\vec{p}_{\bot}$ only in terms of $\vec{t}$, $\vec{l}$, and the rotation angle $\theta$. Next, proceed in a similar manner as the derivation of equations $(2)$ to $(5)$ in post Mozzi-Chasles' Screw Theorem, Half-Turn Equivalence and Combining Successive Screw Displacements.

For $\vec{p_2}+\vec{p_1}$, begin by using the relation

$$ \tan{\Big(\frac{\theta}{2}\Big)} = \frac{\Vert \vec{p_2} - \vec{p_1} \Vert}{\Vert \vec{p_2} + \vec{p_1} \Vert}$$

then cross-multiplying $\vec{p_2}-\vec{p_1}$ with the unit vector $\vec{l}$ to get:

$$ \vec{p_2}+\vec{p_1} = \cot{\Big(\frac{\theta}{2}\Big)} \Big(\vec{p_2}-\vec{p_1}\Big) \times \vec{l}$$

The vector that is half the length of $ \vec{p_2}+\vec{p_1}$ but in the opposite direction from the bisecting point $\mathrm{B}$ to point $\mathrm{P}$ at the tip of $\vec{p}_{\bot}$ is:

$$ -\frac{1}{2}\Big(\vec{p_2}+\vec{p_1}\Big) = \frac{1}{2} \cot{\Big(\frac{\theta}{2}\Big)}\vec{l}\times\Big(\vec{p_2}-\vec{p_1}\Big)$$

and because

$$ \Big(\vec{p_2}-\vec{p_1}\Big) = \vec{t} - \Big(\vec{t}\cdot\vec{l} \Big) \vec{l}$$

then we get

$$ -\frac{1}{2}\Big(\vec{p_2}+\vec{p_1}\Big) = \frac{1}{2} \cot{\Big(\frac{\theta}{2}\Big)}\vec{l}\times\vec{t}$$

From Figure 1 we see that three successive vectors, the first starting from the coordinate system origin to the mid-point of $\vec{t}$, then the second from the mid-point of $\vec{t}$ to point $\mathrm{B}$ and finally the third from point $\mathrm{B}$ towards point $\mathrm{P}$, give the same result as $\vec{p}_{\bot}$. So we have:

$$\begin{align} \vec{p}_{\bot} &= \frac{1}{2}\vec{t} - \frac{1}{2}\Big(\vec{t}\cdot\vec{l} \Big) \vec{l} - \frac{1}{2}\Big(\vec{p_2}+\vec{p_1}\Big) \\ &= \frac{1}{2}\vec{t} - \frac{1}{2}\Big(\vec{t}\cdot\vec{l} \Big) \vec{l} + \frac{1}{2} \cot{\Big(\frac{\theta}{2}\Big)}\vec{l}\times\vec{t}\\ &= \frac{1}{2} \bigg(\vec{t} - \Big(\vec{t}\cdot\vec{l} \Big) \vec{l} + \cot{\Big(\frac{\theta}{2}\Big)}\vec{l}\times\vec{t} \bigg) \end{align}$$

Finally, for $\vec{m}$ we have:

$$\vec{m} = \vec{p}_{\bot} \times \vec{l} = \frac{1}{2} \bigg(\vec{t}\times \vec{l} + \cot{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\times\vec{t}\Big)\times \vec{l} \bigg)\tag{5}$$

We know from post Unit Dual Quaternion For Translation And Rotation that we use the dual qauternion rotation and translation operator:

$$\pmb{r_0} + \frac{\epsilon}{2}\vec{t}\pmb{r_0}\tag{6}$$

We recall from equation $(23)$ of the post Extracting the Cross and Dot Products from the Quaternion Rotation Operator that:

$$ \pmb{r_0} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l}\tag{7}$$

Substituting equation $(7)$ into $(6)$ gives:

$$\begin{align} \pmb{r_0} + \frac{\epsilon}{2}\vec{t}\pmb{r_0} &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \frac{\epsilon}{2}\bigg( \cos{\Big(\frac{\theta}{2}\Big)}\vec{t} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{t}\vec{l}\bigg)\\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \frac{\epsilon}{2}\bigg( \cos{\Big(\frac{\theta}{2}\Big)}\vec{t} - \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{t}\cdot\vec{l}\Big) + \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{t}\times\vec{l}\Big)\bigg)\tag{8}\\ \end{align}$$

Now let's multiply both sides of equation $(5)$ by $\sin{\big(\frac{\theta}{2} \big)}$:

$$\sin{\Big(\frac{\theta}{2} \Big)}\vec{m} = \frac{1}{2} \bigg(\sin{\Big(\frac{\theta}{2} \Big)}\Big(\vec{t}\times \vec{l}\Big) + \cos{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\times\vec{t}\Big)\times \vec{l} \bigg)\tag{9}$$

rearranging $(9)$:

$$\sin{\Big(\frac{\theta}{2} \Big)}\Big(\vec{t}\times \vec{l}\Big) = 2\sin{\Big(\frac{\theta}{2} \Big)}\vec{m} - \cos{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\times\vec{t}\Big)\times \vec{l}\tag{10}$$

Substituting $(10)$ into $(8)$ gives:

$$\begin{align} \pmb{r_0} + \frac{\epsilon}{2}&\vec{t}\pmb{r_0}\\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l}\\ &+ \frac{\epsilon}{2}\bigg( \cos{\Big(\frac{\theta}{2}\Big)}\vec{t} - \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{t}\cdot\vec{l}\Big) + 2\sin{\Big(\frac{\theta}{2} \Big)}\vec{m} - \cos{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\times\vec{t}\Big)\times \vec{l}\bigg)\\\\ &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l}\\ &+ \frac{\epsilon}{2}\bigg( \cos{\Big(\frac{\theta}{2}\Big)}\vec{t} - \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{t}\cdot\vec{l}\Big) + 2\sin{\Big(\frac{\theta}{2} \Big)}\vec{m} + \cos{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\cdot\vec{t}\Big)\vec{l} - \cos{\Big(\frac{\theta}{2}\Big)}\vec{t}\bigg)\\\\ &= \cos{\Big(\frac{\theta}{2}\Big)} - \frac{\epsilon}{2}\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{t}\cdot\vec{l}\Big)\\ &+ \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\bigg( \sin{\Big(\frac{\theta}{2} \Big)}\vec{m} + \frac{1}{2}\cos{\Big(\frac{\theta}{2}\Big)}\Big(\vec{l}\cdot\vec{t}\Big)\vec{l}\bigg)\\ \\ &= \cos{\Big(\frac{\theta}{2}\Big)} - \epsilon\frac{d}{2}\sin{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\bigg(\sin{\Big(\frac{\theta}{2}\Big)}\vec{m} + \frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)}\vec{l} \bigg)\tag{11} \end{align}$$

Equations $(4)$ and $(11)$ are the same and can be simplified further since a Taylor series expansion of every function $f$ of dual numbers yeilds the rule that:

$$ f\big(a + \epsilon b \big) = f\big(a\big) + \epsilon b f^{'}\big(a\big)$$

hence

$$\begin{align} \cos{\Big(\frac{\theta + \epsilon d}{2}\Big)} &= \cos{\Big(\frac{\theta}{2}\Big)} - \epsilon\frac{d}{2}\sin{\Big(\frac{\theta}{2}\Big)}\\ \sin{\Big(\frac{\theta + \epsilon d}{2}\Big)} &= \sin{\Big(\frac{\theta}{2}\Big)} + \epsilon\frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)} \end{align}$$

Letting $\sigma = \pmb{r_0} + \frac{\epsilon}{2}\vec{t}\pmb{r_0}$ and substituting the two equations above into $(4)$ or $(11)$ gives us:

$$\begin{align} \sigma &= \pmb{r_0} + \frac{\epsilon}{2}\vec{t}\pmb{r_0}\\ &=\cos{\Big(\frac{\theta + \epsilon d}{2}\Big)} + \bigg(\sin{\Big(\frac{\theta}{2}\Big)} + \epsilon\frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)}\bigg)\vec{l} + \sin{\Big(\frac{\theta}{2}\Big)}\epsilon\vec{m}\\ &=\cos{\Big(\frac{\theta + \epsilon d}{2}\Big)} + \bigg(\sin{\Big(\frac{\theta}{2}\Big)} + \epsilon\frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)}\bigg)\vec{l} + \bigg(\sin{\Big(\frac{\theta}{2}\Big)} + \epsilon\frac{d}{2}\cos{\Big(\frac{\theta}{2}\Big)}\bigg)\epsilon\vec{m}\\ &= \cos{\Big(\frac{\theta + \epsilon d}{2}\Big)} + \sin{\Big(\frac{\theta + \epsilon d}{2}\Big)}\Big(\vec{l} + \epsilon\vec{m} \Big)\tag{12} \end{align}$$

By introducing the following dual angle and dual vector

$$\begin{align} \bar{\theta} &= \theta + \epsilon d \\ \bar{\vec{l}} &= \vec{l} + \epsilon\vec{m} \end{align}$$

then equation $(12)$ can be rewritten into a very succinct form:

$$\sigma = \cos{\Big(\frac{\bar{\theta}}{2}\Big)} + \bar{\vec{l}}\sin{\Big(\frac{\bar{\theta}}{2}\Big)}\tag{13} $$

IGNORE BELOW.

Applying the dual quaternion displacement operator to the Plücker Coordinates

$$\begin{align} \pmb{\hat{s}}\big(\vec{l} + \epsilon\vec{m}\big)\pmb{\bar{\hat{s}}^{*}} &= \big(\pmb{r_0} + \frac{\epsilon}{2}\vec{d}\pmb{r_0}\big)\big( \vec{l} + \epsilon\vec{m}\big)\big( \pmb{{r_0}^{*}} - \frac{\epsilon}{2}\pmb{{r_0}^{*}}\vec{d}^{*}\big) \\ &= \big(\pmb{r_0}\vec{l} + \epsilon\pmb{r_0}\vec{m} + \frac{\epsilon}{2}\vec{d}\pmb{r_0}\vec{l}\big)\big( \pmb{{r_0}^{*}} - \frac{\epsilon}{2}\pmb{{r_0}^{*}}\vec{d}^{*}\big)\\ &= \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} - \frac{\epsilon}{2}\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\vec{d}^{*} + \epsilon\pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \frac{\epsilon}{2}\vec{d}\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\\ &= \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} + \epsilon\bigg(\pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \frac{1}{2}\Big(\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\vec{d}^{*} + \vec{d}\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\Big) \bigg)\tag{2} \\ \end{align}$$

Letting $\vec{l^{'}} + \epsilon\vec{m^{'}} = \pmb{\hat{s}}\big(\vec{l} + \epsilon\vec{m}\big)\pmb{\bar{\hat{s}}^{*}}$ then:

$$\begin{align} \vec{l^{'}} &= \pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\tag{3} \\ \vec{m^{'}} &= \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \frac{1}{2}\Big( \pmb{r_0} \vec{l} \pmb{{r_0}^{*}} \vec{d}^{*} + \vec{d}\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\Big) \\ &= \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \frac{1}{2}\bigg( \Big(\pmb{r_0} \vec{l} \pmb{{r_0}^{*}}\Big) \cdot \vec{d} - \Big(\pmb{r_0} \vec{l} \pmb{{r_0}^{*}} \times \vec{d}\Big) - \vec{d} \cdot \Big(\pmb{r_0} \vec{l} \pmb{{r_0}^{*}}\Big) + \Big(\vec{d} \times \pmb{r_0} \vec{l} \pmb{{r_0}^{*}} \Big)\bigg) \\ &= \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \vec{d} \times \pmb{r_0} \vec{l} \pmb{{r_0}^{*}}\tag{4} \\ \end{align}$$

Therfore

$$\vec{l^{'}} + \epsilon\vec{m^{'}} = \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} + \epsilon\Big( \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \vec{d} \times \pmb{r_0} \vec{l} \pmb{{r_0}^{*}} \Big)\tag{5}$$

In terms of $\theta$ we use equation $(23)$ from Extracting the Cross and Dot Products from the Quaternion Rotation Operator and have

$$\begin{align} \vec{l^{'}} &= \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} \\ \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{m} \end{align}$$ which are substituted into $(4)$ above to give:

$$\begin{align} \vec{m^{'}} &= \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{m} + \cos{\Big(\frac{\theta}{2}\Big)}\vec{d} + \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{d}\times\vec{l}\Big)\tag{6} \\ \end{align}$$

Therefore:

$$\vec{l^{'}} + \epsilon\vec{m^{'}} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{l} + \epsilon\bigg(\cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{m} + \cos{\Big(\frac{\theta}{2}\Big)}\vec{d} + \sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{d}\times\vec{l}\Big)\bigg)\tag{7}$$

Since $\vec{m} = \vec{p}\times\vec{l}$ in equation $(6)$, let's first look at what happens to $\vec{p}$ with transformation. From equation $(7)$ in Unit Dual Quaternion For Translation And Rotation, we have for $1 + \epsilon\vec{p}$:

$$1 + \epsilon\vec{p^{'}} = 1 + \epsilon\big(\pmb{r_0}\vec{p}\pmb{{r_0}^{*}} + \vec{d}\big)$$

and therefore:

$$\vec{p^{'}} = \pmb{r_0}\vec{p}\pmb{{r_0}^{*}} + \vec{d}$$

Now since vectors $\vec{l}$ and $\vec{p}$ are rotated around the same axis by the same amount then their cross-product $\vec{m}$ is as well so $\pmb{r_0}\vec{m}\pmb{{r_0}^{*}} = \pmb{r_0}\big(\vec{p}\times\vec{l}\big)\pmb{{r_0}^{*}} = \pmb{r_0}\vec{p}\pmb{{r_0}^{*}} \times \pmb{r_0}\vec{l}\pmb{{r_0}^{*}}$ and:

$$\begin{align} \vec{m^{'}} &= \vec{p^{'}}\times\vec{l^{'}} \\ &= \Big( \pmb{r_0}\vec{p}\pmb{{r_0}^{*}} + \vec{d} \Big) \times \Big( \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} \Big) \\ &= \pmb{r_0}\vec{p}\pmb{{r_0}^{*}} \times \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} + \vec{d} \times \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} \\ &= \pmb{r_0}\vec{m}\pmb{{r_0}^{*}} + \vec{d} \times \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} \end{align}$$

Since the cross-product of two pure quaternions $\vec{a}$ and $\vec{b}$ is $\vec{a}\times\vec{b} = \frac{1}{2}\Big(\vec{b}\vec{a}^{*} + \vec{a}\vec{b} \Big)$ then:

$$ \vec{d} \times \pmb{r_0}\vec{l}\pmb{{r_0}^{*}} = \frac{1}{2}\Big(\pmb{r_0}\vec{l}\pmb{{r_0}^{*}}\vec{d}^{*} + \vec{d}^{*}\pmb{r_0}\vec{l}\pmb{{r_0}^{*}} \Big)$$

Extracting the Cross and Dot Products from the Quaternion Rotation Operator

The product of two regular quaternions $\pmb{r} = r_0 + \vec{r}$ and $\pmb{v} = 0 + \vec{v}$ is:

$$\begin{align} \pmb{r}\vec{v} &= \big( r_0 + \vec{r}\big)\big(\vec{v} \big) \\ &= \big( r_0 + r_x\vec{i}+ r_y\vec{j} + r_z\vec{k}\big)\big(v_x\vec{i}+ v_y\vec{j} + v_z\vec{k} \big) \\ \\ &= r_{0}v_{x}\vec{i} + r_{0}v_{y}\vec{j} + r_{0}v_{z}\vec{k} \\ &\quad - r_{x}v_{x} + r_{x}v_{y}\vec{k} - r_{x}v_{z}\vec{j} \\ &\quad - r_{y}v_{x}\vec{k} - r_{y}v_{y} + r_{y}v_{z}\vec{i} \\ &\quad + r_{z}v_{x}\vec{j} - r_{z}v_{y}\vec{i} - r_{z}v_{z} \tag{1} \end{align}$$

Rearranging the terms in equation $\big(1\big)$ as follows:

$$\begin{align} \pmb{r}\vec{v} &= -\big(r_{x}v_{x} + r_{y}v_{y} + r_{z}v_{z}\big) \\ &\quad+ r_{0}\big(v_{x}\vec{i} + v_{y}\vec{j} + v_{z}\vec{k}\big) \\ &\quad+ \big(r_{y}v_{z} - r_{z}v_{y}\big)\vec{i} + \big(r_{z}v_{x} - r_{x}v_{z} \big)\vec{j} + \big( r_{x}v_{y} - r_{y}v_{x}\big)\vec{k}\tag{2} \\ \\ &= - \vec{r}\cdot\vec{v} + r_{0}\vec{v} + \vec{r} \times \vec{v} \tag{3} \end{align}$$

Right multiplying equation $\big(3\big)$ by the conjugate $\pmb{r}^{*} = r_{0} - \vec{r}$ gives:

$$\begin{align} \pmb{r}\vec{v}\pmb{r}^{*} &= \big(- \vec{r}\cdot\vec{v} + r_{0}\vec{v} + \vec{r} \times \vec{v}\big)\big(r_{0} - \vec{r} \big) \\ &= -(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \big(\vec{v}r_{0} + (\vec{r} \times \vec{v})\big)r_{0} + \big(\vec{v}r_{0} + (\vec{r} \times \vec{v})\big)(-\vec{r}) \\ &= -(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \vec{v}r_{0}^2 + (\vec{r} \times \vec{v})r_{0} +\vec{v}r_{0}(-\vec{r} ) + (\vec{r} \times \vec{v})(-\vec{r})\tag{4} \\ \end{align}$$

Expanding and rearranging the term $(\vec{r} \times \vec{v})(-\vec{r})$ and letting $\vec{m} = \vec{r} \times \vec{v}$:

$$\begin{align} (\vec{r} \times \vec{v})(-\vec{r})&= \big(r_{y}v_{z} - r_{z}v_{y}\big)\vec{i}\big( r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big) \\ &\quad+ \big(r_{z}v_{x} - r_{x}v_{z} \big)\vec{j}\big( r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big) \\ &\quad+ \big( r_{x}v_{y} - r_{y}v_{x}\big)\vec{k}\big(r_0 - r_x\vec{i}- r_y\vec{j} - r_z\vec{k} \big)\tag{5} \\ \\ &= m_{x}r_0\vec{i} + m_{x}r_x - m_{x}r_y\vec{k} + m_{x}r_z\vec{j} \\ &\quad+ m_{y}r_0\vec{j} + m_{y}r_x\vec{k} + m_{y}r_y - m_{y}r_z\vec{i} \\ &\quad+ m_{z}r_0\vec{k} - m_{z}r_x\vec{j} + m_{z}r_y\vec{i} + m_{z}r_z\tag{6} \\ \\ &= m_{x}r_x + m_{y}r_y + m_{z}r_z \\ &\quad+ r_0\big(m_{x}\vec{i} + m_{y}\vec{j} + m_{z}\vec{k}\big) \\ &\quad+ \big(m_{z}r_y - m_{y}r_z\big)\vec{i} + \big(m_{x}r_z - m_{z}r_x \big)\vec{j} + \big(m_{y}r_x - m_{x}r_y \big)\vec{k}\tag{7} \\ \\ &= \big(\vec{r} \times \vec{v}\big) \cdot \vec{r} + r_{0}\big(\vec{r} \times \vec{v}\big) - \big(\vec{r} \times \vec{v}\big)\times\vec{r}\tag{8} \end{align}$$

The following term has this vector triple product expansion:

$$\begin{align} \big(\vec{r} \times \vec{v}\big)\times\vec{r} &= -\big(\vec{r}\cdot\vec{v}\big)\vec{r} + \big(\vec{r}\cdot\vec{r}\big)\vec{v} \\ &= -\big(\vec{r}\cdot\vec{v}\big)\vec{r} + \Vert\vec{r}\Vert^2\vec{v} \end{align}$$

Since $\big(\vec{r} \times \vec{v}\big) \cdot \vec{r} = 0$ then $(8)$ becomes:

$$(\vec{r} \times \vec{v})(-\vec{r} )= r_{0}\big(\vec{r} \times \vec{v}\big)+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{9}$$

Expanding and rearranging $\vec{v}(-\vec{r})$ in the term $\vec{v}r_{0}(-\vec{r})$:

$$\begin{align} \vec{v}(-\vec{r}) &= \big(v_{x}\vec{i} + v_{y}\vec{j} + v_{z}\vec{k}\big)\big(-r_{x}\vec{i} - r_{y}\vec{j} - r_{z}\vec{z} \big) \\ &= v_{x}r_{x} - v_{x}r_{y}\vec{k} + v_{x}r_{z}\vec{j} \\ &\quad v_{y}r_{x}\vec{k} + v_{y}r_{y} - v_{y}r_{z}\vec{i} \\ &\quad -v_{z}r_{x}\vec{j} + v_{z}r_{y}\vec{i} + v_{z}r_{z} \\ \\ &= \big(v_{x}r_{x} + v_{y}r_{y} + v_{z}r_{z}\big) \\ &\quad +\big(-v_{y}r_{z} + v_{z}r_{y}\big)\vec{i} + \big(-v_{z}r_{x} + v_{x}r_{z}\big)\vec{j}+\big(-v_{x}r_{y} + v_{y}r_{x}\big)\vec{k} \\ \\ &= \vec{v}\cdot \vec{r} - \vec{v} \times \vec{r} \\ &= \vec{r}\cdot \vec{v} + \vec{r} \times \vec{v}\tag{10} \end{align}$$

The terms $\vec{v}r_{0}(-\vec{r}) +(\vec{r} \times \vec{v})(-\vec{r})$ in $(4)$ then become:

$$\begin{align} \vec{v}r_{0}(-\vec{r}) +(\vec{r} \times \vec{v})(-\vec{r}) &= r_{0}(\vec{r}\cdot \vec{v}) + r_{0}(\vec{r} \times \vec{v}) +r_{0}\big(\vec{r} \times \vec{v}\big)+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v} \\ &= r_{0}(\vec{r}\cdot \vec{v}) + 2r_{0}(\vec{r} \times \vec{v})+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{11} \end{align}$$

Substituting $\big(11\big)$ into equation $\big(4\big)$:

$$-(\vec{r}\cdot\vec{v})r_{0} + (\vec{r}\cdot\vec{v})\vec{r} + \vec{v}r_{0}^2 + (\vec{r} \times \vec{v})r_{0} +r_{0}(\vec{r}\cdot \vec{v}) + 2r_{0}(\vec{r} \times \vec{v})+\big(\vec{r}\cdot\vec{v}\big)\vec{r} - \Vert\vec{r}\Vert^2\vec{v}\tag{12}$$

Reducing $\big(12\big)$ gives the pure quaternion:

$$\pmb{r}\vec{v}\pmb{r}^{*} = \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\vec{v} +2\big(\vec{r}\cdot\vec{v}\big)\vec{r} + 2r_{0}\big(\vec{r}\times\vec{v}\big)\tag{13}$$

Next we need to find out what rotation the unit quaternion $\pmb{r}$ represents. Substituting $\vec{r}$ for $\vec{v}$ in $\big(13\big)$ makes $\vec{v} = \vec{r}$ collinear with the axis of rotation and yields:

$$\begin{align} \pmb{r}\vec{v}\pmb{r}^{*} &= \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\vec{v} +2\big(\vec{r}\cdot\vec{v}\big)\vec{r} + 2r_{0}\big(\vec{r}\times\vec{v}\big)\\ &= \big(r_{0}^2+\Vert\vec{r}\Vert^2\big)\vec{r}\\ &= \vec{r}\tag{14} \end{align}$$

As it should, $\pmb{r}\vec{v}\pmb{r}^{*}$ remains the same as $\vec{r}$ after the rotation.

Finally, we need to determine the angle of rotation $\theta$. Let the vector $\vec{v}$ be perpendicular to the axis of rotation and then turned into a vector $\vec{{v}^{'}}$ making an angle $\theta$ with $\vec{v}$. In Figure 1 the position vector $\vec{a}$ is associated with $\vec{v}$ and then choosing $\vec{v} = \vec{r} \times \vec{a}$ where $\vec{a}$ is not parallel to $\vec{r}$ gives:

$$\vec{{v}^{'}} = \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\big(\vec{r} \times \vec{a}\big) +2\big(\vec{r}\cdot\big(\vec{r} \times \vec{a}\big)\big)\vec{r} + 2r_{0}\big(\vec{r}\times\big(\vec{r} \times \vec{a}\big)\big)\tag{15}$$

Figure 1

We find that

$$\begin{align} \vec{v}\cdot\vec{{v}^{'}} &=\big(\vec{r} \times \vec{a}\big)\cdot\Big( \big(r_{0}^2-\Vert\vec{r}\Vert^2\big)\big(\vec{r} \times \vec{a}\big) +2\big(\vec{r}\cdot\big(\vec{r} \times \vec{a}\big)\big)\vec{r} + 2r_{0}\big(\vec{r}\times\big(\vec{r} \times \vec{a}\big)\big) \Big) \\ &= \big(r_{0}^{2} - \Vert\vec{r}\Vert^{2} \big)\Vert \vec{r} \times \vec{a} \Vert^{2}\\ &= \big(r_{0}^{2} - \Vert\vec{r}\Vert^{2} \big)\Vert v \Vert^{2}\tag{16} \end{align}$$

Since $\Vert \vec{{v}^{'}} \Vert = \Vert \vec{v} \Vert$ and $\vec{v}\cdot\vec{{v}^{'}} = \Vert \vec{{v}^{'}} \Vert \Vert \vec{v} \Vert\cos{(\theta)}$ then

$$r_{0}^{2} - \Vert\vec{r}\Vert^{2} = \cos{(\theta)}\tag{17}$$

Noting that $\pmb{r}$ is a unit quaternion then $r_{0}^{2} + \Vert\vec{r}\Vert^{2} = 1$ and this is added to $\big(17\big)$:

$$\begin{align} r_{0}^{2} + \Vert\vec{r}\Vert^{2} + r_{0}^{2} - \Vert\vec{r}\Vert^{2} &= 1 + \cos{(\theta)}\\ 2r_{0}^{2} &= 1 + \cos{(\theta)}\tag{18} \end{align}$$

Using the trigonometric half-angle formula $\cos^2{\Big(\frac{\theta}{2}\Big)} = \frac{1 + \cos{(\theta)}}{2}$ on $\big(18\big)$ gives:

$$r_{0} = \pm\cos{\Big(\frac{\theta}{2}\Big)}\tag{19}$$

Now if $\big(17\big)$ is subtracted from $r_{0}^{2} + \Vert\vec{r}\Vert^{2} = 1$ then:

$$\begin{align} r_{0}^{2} + \Vert\vec{r}\Vert^{2} - r_{0}^{2} + \Vert\vec{r}\Vert^{2} &= 1 - \cos{(\theta)}\\ 2\Vert\vec{r}\Vert^{2} &= 1 - \cos{(\theta)}\tag{20} \end{align}$$

Using the trigonometric half-angle formula $\sin^2{\Big(\frac{\theta}{2}\Big)} = \frac{1 - \cos{(\theta)}}{2}$ on $\big(20\big)$ gives:

$$\Vert\vec{r}\Vert= \sin{\Big(\frac{\theta}{2}\Big)}\tag{21}$$

Let $\vec{u}$ be the unit direction vector of the axis of rotation and $\vec{r}$:

$$\vec{r} = \pm\sin{\Big(\frac{\theta}{2}\Big)}\vec{u}\tag{22}$$

Finally

$$\pmb{r} = \cos{\Big(\frac{\theta}{2}\Big)} + \sin{\Big(\frac{\theta}{2}\Big)}\vec{u}\tag{23}$$

Using equations $(13)$, $(19)$ and $(22)$ with the trigonometric identities:

$$\begin{align} \cos^{2}{\Big(\frac{\theta}{2}\Big)} - \sin^{2}{\Big(\frac{\theta}{2}\Big)} &= \cos{\big(\theta\big)}\\ 2\sin{\Big(\frac{\theta}{2}\Big)}\cos{\Big(\frac{\theta}{2}\Big)} &= \sin{\big(\theta\big)}\\ \sin^2{\Big(\frac{\theta}{2}\Big)} &= \frac{1 - \cos{(\theta)}}{2} \end{align}$$

we obtain the Rodrigues' rotation formula:

$$\begin{align} \vec{{v}^{'}} &=\bigg( \cos^2{\Big(\frac{\theta}{2}\Big)} - \sin^{2}{\Big(\frac{\theta}{2}\Big)} \bigg)\vec{v} + 2\cos{\Big(\frac{\theta}{2}\Big)}\sin{\Big(\frac{\theta}{2}\Big)}\Big(\vec{u} \times \vec{v} \Big)+ 2\sin^2{\Big(\frac{\theta}{2}\Big)}\Big( \vec{u}\cdot \vec{v}\Big)\vec{u}\\ &= \cos{(\theta)}\vec{v} + \sin{(\theta)}\big(\vec{u} \times \vec{v}\big) + \big(1 - \cos{(\theta)}\big)\big(\vec{u} \cdot \vec{v}\big)\vec{u}\tag{24} \end{align}$$